Rows: 48
Columns: 5
$ density <int> 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 1…
$ pred <fct> no, no, no, no, no, no, no, no, pred, pred, pred, pred, pred,…
$ size <fct> big, big, big, big, small, small, small, small, big, big, big…
$ surv <int> 9, 10, 7, 10, 9, 9, 10, 9, 4, 9, 7, 6, 7, 5, 9, 9, 24, 23, 22…
$ propsurv <dbl> 0.90, 1.00, 0.70, 1.00, 0.90, 0.90, 1.00, 0.90, 0.40, 0.90, 0…Statistical Rethinking Week 8
This week was our first introduction to Multilevel models. Models where we explicitly model a family of parameters as coming from a common distribution: with each sample, we simultaneously learn each parameter and the parameters of the common distribution. This process of sharing information is called pooling. The end result is shrinkage: each parameter gets pulled towards the estimated mean of the common distribution. I tried my best to understand this process and result by simulating in this post
Homework
1st Problem
Revisit the Reed frog survival data, data(reedfrogs), and add the predation and size treatment variables to the varying intercepts model. Consider models with either predictor alone, both predictors, as well as a model including their interaction. What do you infer about the causal influence of these predictor variables? Also focus on the inferred variation across tanks (the \(\sigma\) across tanks). Explain why it changes as it does across models with different predictors included.
Model with only predation
Let’s check how the predation variable is encoded:
pred n
1 no 24
2 pred 24 predation_int pred n
1 0 no 24
2 1 pred 24Now, let’s propose the model with varying intercept for tanks and taking into account whether there were predators or not.
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 2000 [ 5%] (Warmup)
Chain 1 Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 1 Iteration: 300 / 2000 [ 15%] (Warmup)
Chain 2 Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 2000 [ 5%] (Warmup)
Chain 2 Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 2 Iteration: 300 / 2000 [ 15%] (Warmup)
Chain 2 Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 2 Iteration: 500 / 2000 [ 25%] (Warmup)
Chain 2 Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 3 Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 2000 [ 5%] (Warmup)
Chain 3 Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 3 Iteration: 300 / 2000 [ 15%] (Warmup)
Chain 3 Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 3 Iteration: 500 / 2000 [ 25%] (Warmup)
Chain 3 Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 4 Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 2000 [ 5%] (Warmup)
Chain 4 Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 4 Iteration: 300 / 2000 [ 15%] (Warmup)
Chain 4 Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 4 Iteration: 500 / 2000 [ 25%] (Warmup)
Chain 4 Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 1 Iteration: 500 / 2000 [ 25%] (Warmup)
Chain 1 Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1 Iteration: 700 / 2000 [ 35%] (Warmup)
Chain 1 Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 1 Iteration: 900 / 2000 [ 45%] (Warmup)
Chain 1 Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 1 Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 1 Iteration: 1100 / 2000 [ 55%] (Sampling)
Chain 2 Iteration: 700 / 2000 [ 35%] (Warmup)
Chain 2 Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 2 Iteration: 900 / 2000 [ 45%] (Warmup)
Chain 2 Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 2 Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 3 Iteration: 700 / 2000 [ 35%] (Warmup)
Chain 3 Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 3 Iteration: 900 / 2000 [ 45%] (Warmup)
Chain 3 Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 3 Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 4 Iteration: 700 / 2000 [ 35%] (Warmup)
Chain 4 Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 4 Iteration: 900 / 2000 [ 45%] (Warmup)
Chain 4 Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 4 Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 1 Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 1 Iteration: 1300 / 2000 [ 65%] (Sampling)
Chain 1 Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 2 Iteration: 1100 / 2000 [ 55%] (Sampling)
Chain 2 Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 2 Iteration: 1300 / 2000 [ 65%] (Sampling)
Chain 3 Iteration: 1100 / 2000 [ 55%] (Sampling)
Chain 3 Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 3 Iteration: 1300 / 2000 [ 65%] (Sampling)
Chain 4 Iteration: 1100 / 2000 [ 55%] (Sampling)
Chain 4 Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 4 Iteration: 1300 / 2000 [ 65%] (Sampling)
Chain 1 Iteration: 1500 / 2000 [ 75%] (Sampling)
Chain 1 Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 2 Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 2 Iteration: 1500 / 2000 [ 75%] (Sampling)
Chain 2 Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 3 Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 3 Iteration: 1500 / 2000 [ 75%] (Sampling)
Chain 4 Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 4 Iteration: 1500 / 2000 [ 75%] (Sampling)
Chain 4 Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 1 Iteration: 1700 / 2000 [ 85%] (Sampling)
Chain 1 Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 1 Iteration: 1900 / 2000 [ 95%] (Sampling)
Chain 2 Iteration: 1700 / 2000 [ 85%] (Sampling)
Chain 2 Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 2 Iteration: 1900 / 2000 [ 95%] (Sampling)
Chain 3 Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 3 Iteration: 1700 / 2000 [ 85%] (Sampling)
Chain 3 Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 4 Iteration: 1700 / 2000 [ 85%] (Sampling)
Chain 4 Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 4 Iteration: 1900 / 2000 [ 95%] (Sampling)
Chain 1 Iteration: 2000 / 2000 [100%] (Sampling)
Chain 2 Iteration: 2000 / 2000 [100%] (Sampling)
Chain 3 Iteration: 1900 / 2000 [ 95%] (Sampling)
Chain 3 Iteration: 2000 / 2000 [100%] (Sampling)
Chain 4 Iteration: 2000 / 2000 [100%] (Sampling)
Chain 1 finished in 0.8 seconds.
Chain 2 finished in 0.7 seconds.
Chain 3 finished in 0.8 seconds.
Chain 4 finished in 0.7 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.7 seconds.
Total execution time: 0.9 seconds.Let’s check the posterior and the Rhat values:
Rhat4
Min. :0.9992
1st Qu.:0.9994
Median :0.9996
Mean :0.9998
3rd Qu.:0.9998
Max. :1.0028 The \(\hat{R}\) values look good enough, all are close to 0. There appear to not be signs of transient like behavior.
mean sd 5.5% 94.5% n_eff Rhat4
pred -1.8222334 0.2997461 -2.280908 -1.312238 1410.822 1.001462
a_bar 2.1963295 0.2296880 1.814582 2.555532 1922.014 1.001507
sigma 0.9106572 0.1645364 0.675735 1.189860 1139.664 1.002823As expected, tanks with predators have, on average, lower log odds of probability of surviving.
Model with only size
Let’s prepare size to the model:
size n
1 big 24
2 small 24 size_int size n
1 0 big 24
2 1 small 24Now, let’s add the size to our model with varying intercepts:
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 2000 [ 5%] (Warmup)
Chain 1 Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 1 Iteration: 300 / 2000 [ 15%] (Warmup)
Chain 1 Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 2 Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 2000 [ 5%] (Warmup)
Chain 2 Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 2 Iteration: 300 / 2000 [ 15%] (Warmup)
Chain 3 Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 2000 [ 5%] (Warmup)
Chain 3 Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 3 Iteration: 300 / 2000 [ 15%] (Warmup)
Chain 4 Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 2000 [ 5%] (Warmup)
Chain 4 Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 1 Iteration: 500 / 2000 [ 25%] (Warmup)
Chain 1 Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1 Iteration: 700 / 2000 [ 35%] (Warmup)
Chain 1 Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 2 Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 2 Iteration: 500 / 2000 [ 25%] (Warmup)
Chain 2 Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 2 Iteration: 700 / 2000 [ 35%] (Warmup)
Chain 3 Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 3 Iteration: 500 / 2000 [ 25%] (Warmup)
Chain 3 Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 3 Iteration: 700 / 2000 [ 35%] (Warmup)
Chain 4 Iteration: 300 / 2000 [ 15%] (Warmup)
Chain 4 Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 4 Iteration: 500 / 2000 [ 25%] (Warmup)
Chain 4 Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1 Iteration: 900 / 2000 [ 45%] (Warmup)
Chain 1 Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 1 Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 1 Iteration: 1100 / 2000 [ 55%] (Sampling)
Chain 2 Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 2 Iteration: 900 / 2000 [ 45%] (Warmup)
Chain 2 Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 2 Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 3 Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 3 Iteration: 900 / 2000 [ 45%] (Warmup)
Chain 3 Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 3 Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 4 Iteration: 700 / 2000 [ 35%] (Warmup)
Chain 4 Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 4 Iteration: 900 / 2000 [ 45%] (Warmup)
Chain 1 Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 1 Iteration: 1300 / 2000 [ 65%] (Sampling)
Chain 2 Iteration: 1100 / 2000 [ 55%] (Sampling)
Chain 2 Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 3 Iteration: 1100 / 2000 [ 55%] (Sampling)
Chain 3 Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 3 Iteration: 1300 / 2000 [ 65%] (Sampling)
Chain 4 Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 4 Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 4 Iteration: 1100 / 2000 [ 55%] (Sampling)
Chain 4 Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 1 Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 1 Iteration: 1500 / 2000 [ 75%] (Sampling)
Chain 1 Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 2 Iteration: 1300 / 2000 [ 65%] (Sampling)
Chain 2 Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 2 Iteration: 1500 / 2000 [ 75%] (Sampling)
Chain 3 Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 3 Iteration: 1500 / 2000 [ 75%] (Sampling)
Chain 4 Iteration: 1300 / 2000 [ 65%] (Sampling)
Chain 4 Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 1 Iteration: 1700 / 2000 [ 85%] (Sampling)
Chain 1 Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 2 Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 2 Iteration: 1700 / 2000 [ 85%] (Sampling)
Chain 3 Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 3 Iteration: 1700 / 2000 [ 85%] (Sampling)
Chain 3 Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 4 Iteration: 1500 / 2000 [ 75%] (Sampling)
Chain 4 Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 1 Iteration: 1900 / 2000 [ 95%] (Sampling)
Chain 1 Iteration: 2000 / 2000 [100%] (Sampling)
Chain 2 Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 2 Iteration: 1900 / 2000 [ 95%] (Sampling)
Chain 2 Iteration: 2000 / 2000 [100%] (Sampling)
Chain 3 Iteration: 1900 / 2000 [ 95%] (Sampling)
Chain 3 Iteration: 2000 / 2000 [100%] (Sampling)
Chain 4 Iteration: 1700 / 2000 [ 85%] (Sampling)
Chain 4 Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 4 Iteration: 1900 / 2000 [ 95%] (Sampling)
Chain 1 finished in 0.8 seconds.
Chain 2 finished in 0.8 seconds.
Chain 3 finished in 0.8 seconds.
Chain 4 Iteration: 2000 / 2000 [100%] (Sampling)
Chain 4 finished in 0.8 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.8 seconds.
Total execution time: 1.0 seconds.Let’s check our \(\hat{R}\) values:
Rhat4
Min. :0.9992
1st Qu.:0.9995
Median :0.9999
Mean :1.0001
3rd Qu.:1.0004
Max. :1.0027 Let’s check our precis ouptut:
mean sd 5.5% 94.5% n_eff Rhat4
s 0.2621837 0.3559195 -0.3168585 0.8315286 1557.368 1.002716
a_bar 1.2242716 0.3072198 0.7418783 1.7224410 1090.394 1.000859
sigma 1.5785150 0.1997810 1.2827567 1.9168341 1338.498 1.002117It seems that the size is not that relevant in the log-odds scale. Its 89% PI covers zero and a prety wide interval.
Model with size and predators
Let’s include both variables:
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 2000 [ 5%] (Warmup)
Chain 2 Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 2000 [ 5%] (Warmup)
Chain 2 Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 3 Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 2000 [ 5%] (Warmup)
Chain 3 Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 4 Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 2000 [ 5%] (Warmup)
Chain 4 Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 1 Iteration: 300 / 2000 [ 15%] (Warmup)
Chain 1 Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 1 Iteration: 500 / 2000 [ 25%] (Warmup)
Chain 2 Iteration: 300 / 2000 [ 15%] (Warmup)
Chain 2 Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 2 Iteration: 500 / 2000 [ 25%] (Warmup)
Chain 2 Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 3 Iteration: 300 / 2000 [ 15%] (Warmup)
Chain 3 Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 3 Iteration: 500 / 2000 [ 25%] (Warmup)
Chain 4 Iteration: 300 / 2000 [ 15%] (Warmup)
Chain 4 Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 1 Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1 Iteration: 700 / 2000 [ 35%] (Warmup)
Chain 2 Iteration: 700 / 2000 [ 35%] (Warmup)
Chain 2 Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 3 Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 3 Iteration: 700 / 2000 [ 35%] (Warmup)
Chain 3 Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 4 Iteration: 500 / 2000 [ 25%] (Warmup)
Chain 4 Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 4 Iteration: 700 / 2000 [ 35%] (Warmup)
Chain 1 Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 1 Iteration: 900 / 2000 [ 45%] (Warmup)
Chain 1 Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 1 Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 2 Iteration: 900 / 2000 [ 45%] (Warmup)
Chain 2 Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 2 Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 2 Iteration: 1100 / 2000 [ 55%] (Sampling)
Chain 3 Iteration: 900 / 2000 [ 45%] (Warmup)
Chain 3 Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 3 Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 4 Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 4 Iteration: 900 / 2000 [ 45%] (Warmup)
Chain 4 Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 4 Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 1 Iteration: 1100 / 2000 [ 55%] (Sampling)
Chain 1 Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 2 Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 2 Iteration: 1300 / 2000 [ 65%] (Sampling)
Chain 3 Iteration: 1100 / 2000 [ 55%] (Sampling)
Chain 3 Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 3 Iteration: 1300 / 2000 [ 65%] (Sampling)
Chain 4 Iteration: 1100 / 2000 [ 55%] (Sampling)
Chain 4 Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 4 Iteration: 1300 / 2000 [ 65%] (Sampling)
Chain 1 Iteration: 1300 / 2000 [ 65%] (Sampling)
Chain 1 Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 1 Iteration: 1500 / 2000 [ 75%] (Sampling)
Chain 2 Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 2 Iteration: 1500 / 2000 [ 75%] (Sampling)
Chain 2 Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 3 Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 3 Iteration: 1500 / 2000 [ 75%] (Sampling)
Chain 4 Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 4 Iteration: 1500 / 2000 [ 75%] (Sampling)
Chain 1 Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 1 Iteration: 1700 / 2000 [ 85%] (Sampling)
Chain 2 Iteration: 1700 / 2000 [ 85%] (Sampling)
Chain 2 Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 2 Iteration: 1900 / 2000 [ 95%] (Sampling)
Chain 3 Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 3 Iteration: 1700 / 2000 [ 85%] (Sampling)
Chain 3 Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 4 Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 4 Iteration: 1700 / 2000 [ 85%] (Sampling)
Chain 4 Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 1 Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 1 Iteration: 1900 / 2000 [ 95%] (Sampling)
Chain 1 Iteration: 2000 / 2000 [100%] (Sampling)
Chain 2 Iteration: 2000 / 2000 [100%] (Sampling)
Chain 3 Iteration: 1900 / 2000 [ 95%] (Sampling)
Chain 3 Iteration: 2000 / 2000 [100%] (Sampling)
Chain 4 Iteration: 1900 / 2000 [ 95%] (Sampling)
Chain 4 Iteration: 2000 / 2000 [100%] (Sampling)
Chain 1 finished in 0.9 seconds.
Chain 2 finished in 0.9 seconds.
Chain 3 finished in 0.9 seconds.
Chain 4 finished in 0.8 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.9 seconds.
Total execution time: 1.0 seconds.Let’s check our \(\hat{R}\) values:
Rhat4
Min. :0.9991
1st Qu.:0.9994
Median :0.9996
Mean :0.9998
3rd Qu.:1.0000
Max. :1.0015 The \(\hat{R}\) values look OK. Let’s check the precis output:
mean sd 5.5% 94.5% n_eff Rhat4
s 0.3802925 0.2658079 -0.04409109 0.7974136 2220.168 1.0014675
pred -1.8502836 0.2942538 -2.29862435 -1.3587384 1648.664 1.0011477
a_bar 2.0230849 0.2598151 1.59480645 2.4302732 2075.647 0.9995557
sigma 0.8718928 0.1674364 0.62479505 1.1597191 1044.173 1.0009064Predators’ effect is still large and negative on the log-odds scale. Also, size’s effect has shifted and, once we have statistically adjusted by the presence of predators, now has most of its posterior mass to the right of zero. Presumably, this arises because size and the presence of predators are related; unless we adjust by the presence of predators, the coefficient for size will pick up some of the predators’ effect.
Model with an interaction
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 2000 [ 5%] (Warmup)
Chain 1 Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 2 Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 2000 [ 5%] (Warmup)
Chain 3 Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 2000 [ 5%] (Warmup)
Chain 4 Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 2000 [ 5%] (Warmup)
Chain 1 Iteration: 300 / 2000 [ 15%] (Warmup)
Chain 1 Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 2 Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 2 Iteration: 300 / 2000 [ 15%] (Warmup)
Chain 2 Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 3 Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 3 Iteration: 300 / 2000 [ 15%] (Warmup)
Chain 3 Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 4 Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 4 Iteration: 300 / 2000 [ 15%] (Warmup)
Chain 4 Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 1 Iteration: 500 / 2000 [ 25%] (Warmup)
Chain 1 Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1 Iteration: 700 / 2000 [ 35%] (Warmup)
Chain 2 Iteration: 500 / 2000 [ 25%] (Warmup)
Chain 2 Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 3 Iteration: 500 / 2000 [ 25%] (Warmup)
Chain 3 Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 4 Iteration: 500 / 2000 [ 25%] (Warmup)
Chain 4 Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1 Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 1 Iteration: 900 / 2000 [ 45%] (Warmup)
Chain 1 Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 1 Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 2 Iteration: 700 / 2000 [ 35%] (Warmup)
Chain 2 Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 2 Iteration: 900 / 2000 [ 45%] (Warmup)
Chain 3 Iteration: 700 / 2000 [ 35%] (Warmup)
Chain 3 Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 3 Iteration: 900 / 2000 [ 45%] (Warmup)
Chain 4 Iteration: 700 / 2000 [ 35%] (Warmup)
Chain 4 Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 4 Iteration: 900 / 2000 [ 45%] (Warmup)
Chain 1 Iteration: 1100 / 2000 [ 55%] (Sampling)
Chain 1 Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 2 Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 2 Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 2 Iteration: 1100 / 2000 [ 55%] (Sampling)
Chain 3 Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 3 Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 3 Iteration: 1100 / 2000 [ 55%] (Sampling)
Chain 4 Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 4 Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 4 Iteration: 1100 / 2000 [ 55%] (Sampling)
Chain 1 Iteration: 1300 / 2000 [ 65%] (Sampling)
Chain 1 Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 2 Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 2 Iteration: 1300 / 2000 [ 65%] (Sampling)
Chain 2 Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 3 Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 3 Iteration: 1300 / 2000 [ 65%] (Sampling)
Chain 4 Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 4 Iteration: 1300 / 2000 [ 65%] (Sampling)
Chain 4 Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 1 Iteration: 1500 / 2000 [ 75%] (Sampling)
Chain 1 Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 1 Iteration: 1700 / 2000 [ 85%] (Sampling)
Chain 2 Iteration: 1500 / 2000 [ 75%] (Sampling)
Chain 2 Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 3 Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 3 Iteration: 1500 / 2000 [ 75%] (Sampling)
Chain 3 Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 4 Iteration: 1500 / 2000 [ 75%] (Sampling)
Chain 4 Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 1 Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 1 Iteration: 1900 / 2000 [ 95%] (Sampling)
Chain 2 Iteration: 1700 / 2000 [ 85%] (Sampling)
Chain 2 Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 3 Iteration: 1700 / 2000 [ 85%] (Sampling)
Chain 3 Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 4 Iteration: 1700 / 2000 [ 85%] (Sampling)
Chain 4 Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 4 Iteration: 1900 / 2000 [ 95%] (Sampling)
Chain 1 Iteration: 2000 / 2000 [100%] (Sampling)
Chain 2 Iteration: 1900 / 2000 [ 95%] (Sampling)
Chain 2 Iteration: 2000 / 2000 [100%] (Sampling)
Chain 3 Iteration: 1900 / 2000 [ 95%] (Sampling)
Chain 3 Iteration: 2000 / 2000 [100%] (Sampling)
Chain 4 Iteration: 2000 / 2000 [100%] (Sampling)
Chain 1 finished in 1.0 seconds.
Chain 2 finished in 1.0 seconds.
Chain 3 finished in 1.0 seconds.
Chain 4 finished in 0.9 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.0 seconds.
Total execution time: 1.1 seconds..
Let’s check on the \(\hat{R}\) values:
Rhat4
Min. :0.9991
1st Qu.:0.9995
Median :0.9997
Mean :0.9999
3rd Qu.:1.0000
Max. :1.0020 The \(\hat{R}\) values look OK. Let’s check the precis output:
mean sd 5.5% 94.5% n_eff Rhat4
s 0.39027815 0.2917359 -0.06399788 0.8527317 2805.604 0.9998481
pred -1.86693961 0.3037439 -2.32497935 -1.3481036 1942.572 1.0012481
interaction -0.01565226 0.2231252 -0.37841780 0.3360543 4759.155 0.9993405
a_bar 2.02130251 0.2554671 1.61979835 2.4199170 2432.114 1.0007998
sigma 0.86186357 0.1669389 0.61695795 1.1412422 1423.359 1.0019521Prediction is still large and negative on the log-odds scale. Size also does not appear to change much with the interaction. The interaction has a large standard error and most of its mass lies largely symmetric around zero.
Now it’s the turn to check how the estimated variation of tanks has changed with the different models:
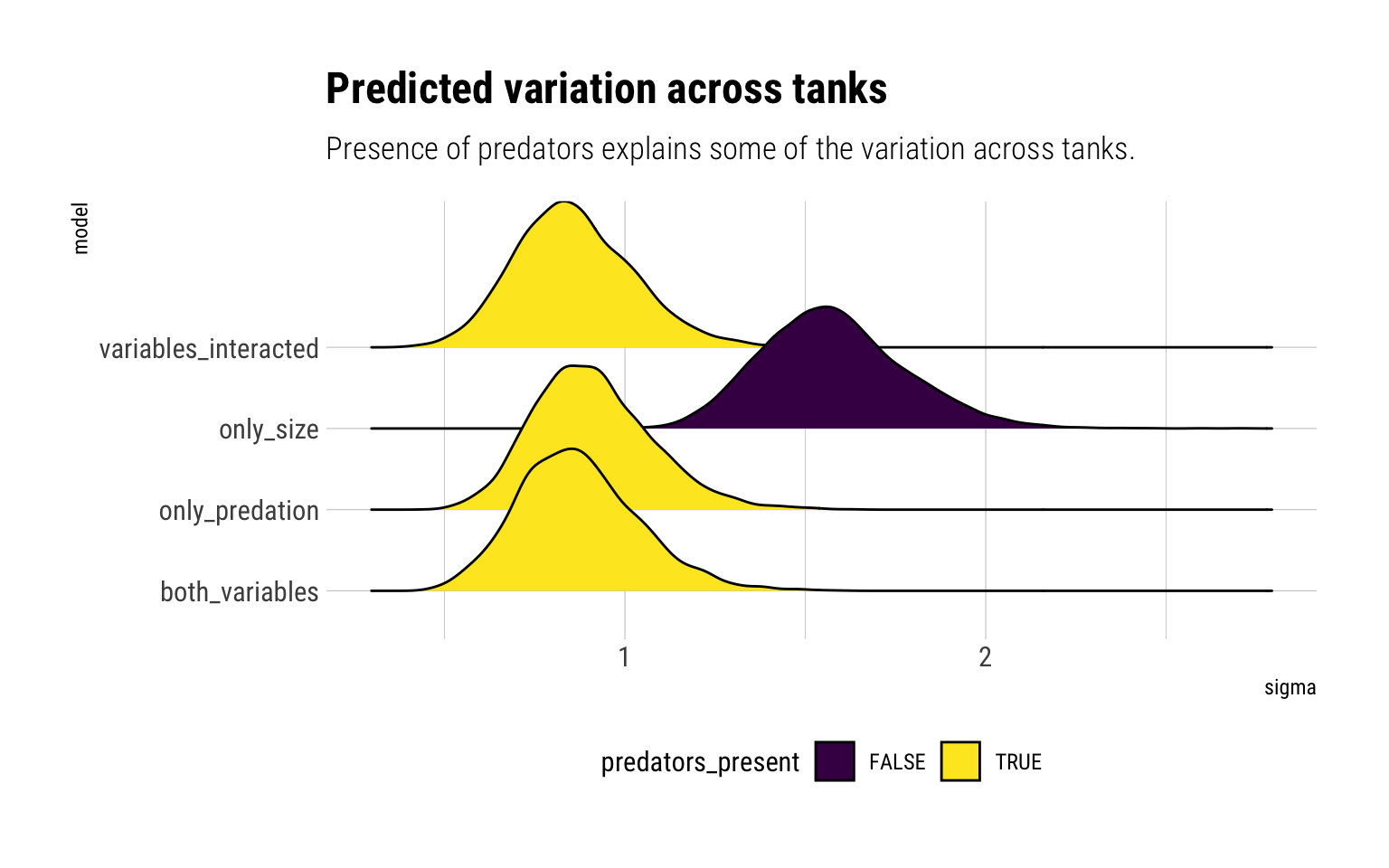
All the models that include predators have almost identical estimates for the variation across tanks. That is, the presence of predators explain some of the variation across tanks.
Finally, let’s compare the models according to information criteria:
WAIC SE dWAIC dSE pWAIC weight
model_both 199.0788 7.927714 0.0000000 NA 19.19389 0.3594406
model_only_predators 199.5214 8.146360 0.4425911 1.5345879 19.53953 0.2880844
model_interaction 200.3865 7.898739 1.3076555 0.5588874 19.65161 0.1869276
model_only_size 200.6294 7.227683 1.5505815 3.9940200 21.08975 0.1655475According to information criteria, all of the models make essentially have the same expected predictive performance out-of-sample.
2nd problem
In 1980, a typical Bengali woman could have 5 or more children in her lifetime. By the year 2000, a typical Bengali woman had only 2 or 3. You’re going to look at a historical set of data, when contraception was widely available but many families chose not to use it. These data reside in data(bangladesh) and come from the 1988 Bangladesh Fertility Survey. Each row is one of 1934 women. There are six variables, but you can focus on two of them for this practice problem:
district
use.contraception
Rows: 1,934
Columns: 6
$ woman <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 1…
$ district <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
$ use.contraception <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1…
$ living.children <int> 4, 1, 3, 4, 1, 1, 4, 4, 2, 4, 1, 1, 2, 4, 4, 4, 1, 4…
$ age.centered <dbl> 18.4400, -5.5599, 1.4400, 8.4400, -13.5590, -11.5600…
$ urban <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…Let’s fix the district:
Now, focus on predicting use.contraception, clustered by district_id. Fit both (1) a traditional fixed-effects model that uses an index variable for district and (2) a multilevel model with varying intercepts for district.
Traditional fixed-effects
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 4.3 seconds.
Chain 2 finished in 4.2 seconds.
Chain 4 finished in 4.2 seconds.
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 finished in 4.3 seconds.
All 4 chains finished successfully.
Mean chain execution time: 4.2 seconds.
Total execution time: 4.4 seconds.Let’s check the \(\hat{R}\) values:
Rhat4
Min. :0.9981
1st Qu.:0.9985
Median :0.9986
Mean :0.9987
3rd Qu.:0.9988
Max. :1.0003 The \(\hat{R}\) values look OK. Let’s fit the multilevel model:
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 5.9 seconds.
Chain 2 finished in 5.9 seconds.
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 finished in 5.9 seconds.
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 finished in 6.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 5.9 seconds.
Total execution time: 6.2 seconds.Let’s check on the \(\hat{R}\) values:
Rhat4
Min. :0.9983
1st Qu.:0.9991
Median :0.9997
Mean :0.9999
3rd Qu.:1.0002
Max. :1.0049 The \(\hat{R}\) values look OK.
Now let’s inspect the values for the distribution of varying intercepts for each district:
mean sd 5.5% 94.5% n_eff Rhat4
alpha -0.5300451 0.09031838 -0.6757211 -0.3845637 725.4713 1.002841
sigma 0.5155339 0.08471016 0.3923543 0.6590001 802.9495 1.002967The overall use of contraceptives seems unlikely across districts, thus the negative alpha.
Plot the predicted proportions of women in each district using contraception, for both the fixed-effects model and the varying-effects model.
Notice that each women, within a same district, has the same prediction.
Let’s average over the posterior the alpha of the distribution of varying intercepts per district
Let’s plot the requested graph:
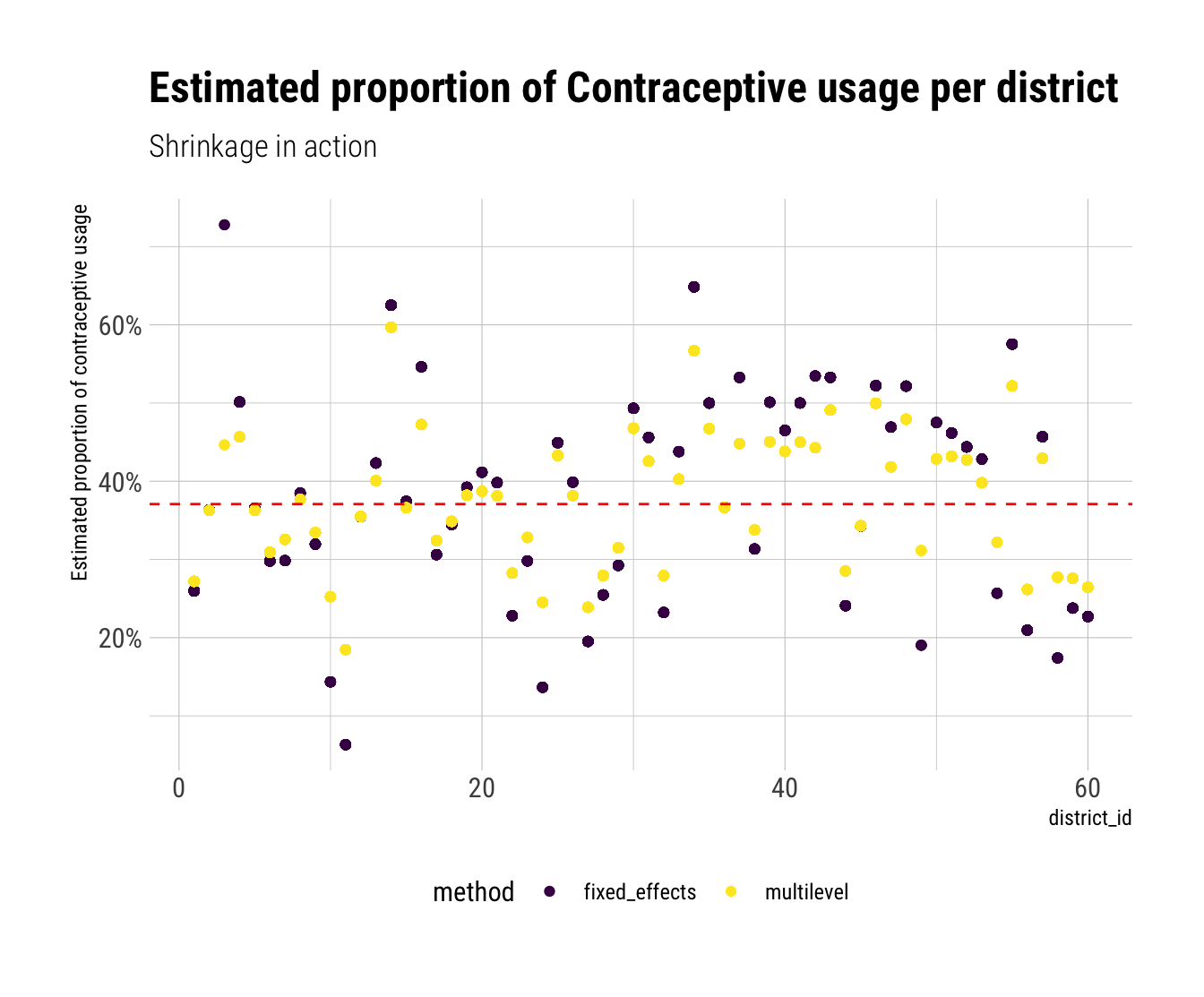
We are seeing the consequences of pooling information from the common distribution of districts: each district’s prediction is overall much closer to the estimated common distribution’s mean than the predictions from the fixed effects model. Therefore, each yellow point is closer to the red line than its corresponding purple point. There are a couple of districts where the difference in predictions between the two models is huge. This are the places where most outside information was used. From what we’ve known about Pooling, these must be the places that were most likely to overfit and had fewer data points. Let’s confirm this intuition:
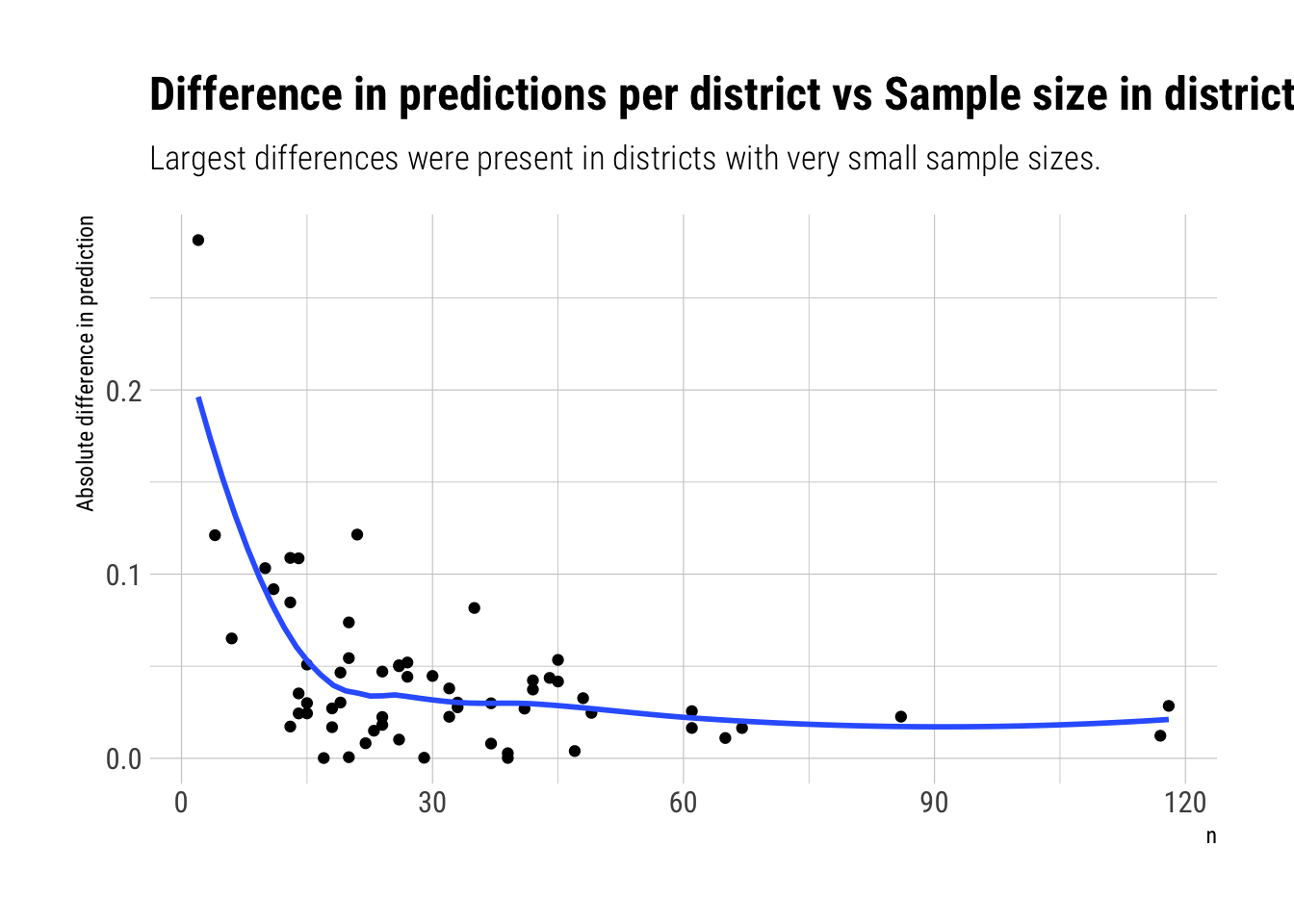
Finally, let’s compare their expected out of sample performance:
WAIC SE dWAIC dSE pWAIC weight
model_multilevel 2515.105 24.92913 0.000000 NA 35.82908 0.98751026
model_fixed_effects 2523.846 28.93510 8.740559 7.733149 53.90337 0.012489743rd Problem
Return to the Trolley data, data(Trolley), from Chapter 12. Define and fit a varying intercepts model for these data. By this I mean to add an intercept parameter for the individual to the linear model. Cluster the varying intercepts on individual participants, as indicated by the unique values in the id variable. Include action, intention, and contact as before.
Rows: 9,930
Columns: 12
$ case <fct> cfaqu, cfbur, cfrub, cibox, cibur, cispe, fkaqu, fkboa, fkbo…
$ response <int> 4, 3, 4, 3, 3, 3, 5, 4, 4, 4, 4, 4, 4, 5, 4, 4, 4, 4, 4, 3, …
$ order <int> 2, 31, 16, 32, 4, 9, 29, 12, 23, 22, 27, 19, 14, 3, 18, 15, …
$ id <fct> 96;434, 96;434, 96;434, 96;434, 96;434, 96;434, 96;434, 96;4…
$ age <int> 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, …
$ male <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ edu <fct> Middle School, Middle School, Middle School, Middle School, …
$ action <int> 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, …
$ intention <int> 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, …
$ contact <int> 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ story <fct> aqu, bur, rub, box, bur, spe, aqu, boa, box, bur, car, spe, …
$ action2 <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, …Therefore, we will run an ordered logistic model where Action, Intention and Contact interact between each other.
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 finished in 238.1 seconds.
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 finished in 255.4 seconds.
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 finished in 265.2 seconds.
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 285.3 seconds.
All 4 chains finished successfully.
Mean chain execution time: 261.0 seconds.
Total execution time: 285.6 seconds.Let’s check our \(\hat{R}\) values:
Rhat4
Min. :1.001
1st Qu.:1.001
Median :1.003
Mean :1.002
3rd Qu.:1.004
Max. :1.004 The \(\hat{R}\) values look good enough.
mean sd 5.5% 94.5% n_eff Rhat4
bIC -1.2536887 0.09787824 -1.4078527 -1.0972498 916.6130 1.001050
bIA -0.4588409 0.07976593 -0.5846241 -0.3308186 915.8706 1.002552
bI -0.2635621 0.05547950 -0.3539045 -0.1741581 851.2259 1.003748
bC -0.3155594 0.06895451 -0.4275243 -0.2047311 881.3079 1.000786
bA -0.4428254 0.05420215 -0.5289409 -0.3556129 798.8642 1.003789Now, let’s fit the model with varying intercepts by individual:
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1500 [ 0%] (Warmup)
Chain 2 Iteration: 1 / 1500 [ 0%] (Warmup)
Chain 3 Iteration: 1 / 1500 [ 0%] (Warmup)
Chain 4 Iteration: 1 / 1500 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 1500 [ 6%] (Warmup)
Chain 4 Iteration: 100 / 1500 [ 6%] (Warmup)
Chain 1 Iteration: 100 / 1500 [ 6%] (Warmup)
Chain 2 Iteration: 100 / 1500 [ 6%] (Warmup)
Chain 3 Iteration: 200 / 1500 [ 13%] (Warmup)
Chain 1 Iteration: 200 / 1500 [ 13%] (Warmup)
Chain 4 Iteration: 200 / 1500 [ 13%] (Warmup)
Chain 2 Iteration: 200 / 1500 [ 13%] (Warmup)
Chain 3 Iteration: 300 / 1500 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1500 [ 20%] (Warmup)
Chain 4 Iteration: 300 / 1500 [ 20%] (Warmup)
Chain 2 Iteration: 300 / 1500 [ 20%] (Warmup)
Chain 3 Iteration: 400 / 1500 [ 26%] (Warmup)
Chain 1 Iteration: 400 / 1500 [ 26%] (Warmup)
Chain 4 Iteration: 400 / 1500 [ 26%] (Warmup)
Chain 3 Iteration: 500 / 1500 [ 33%] (Warmup)
Chain 2 Iteration: 400 / 1500 [ 26%] (Warmup)
Chain 1 Iteration: 500 / 1500 [ 33%] (Warmup)
Chain 4 Iteration: 500 / 1500 [ 33%] (Warmup)
Chain 3 Iteration: 600 / 1500 [ 40%] (Warmup)
Chain 1 Iteration: 600 / 1500 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1500 [ 33%] (Warmup)
Chain 4 Iteration: 600 / 1500 [ 40%] (Warmup)
Chain 3 Iteration: 700 / 1500 [ 46%] (Warmup)
Chain 1 Iteration: 700 / 1500 [ 46%] (Warmup)
Chain 3 Iteration: 751 / 1500 [ 50%] (Sampling)
Chain 4 Iteration: 700 / 1500 [ 46%] (Warmup)
Chain 2 Iteration: 600 / 1500 [ 40%] (Warmup)
Chain 4 Iteration: 751 / 1500 [ 50%] (Sampling)
Chain 1 Iteration: 751 / 1500 [ 50%] (Sampling)
Chain 3 Iteration: 850 / 1500 [ 56%] (Sampling)
Chain 2 Iteration: 700 / 1500 [ 46%] (Warmup)
Chain 4 Iteration: 850 / 1500 [ 56%] (Sampling)
Chain 1 Iteration: 850 / 1500 [ 56%] (Sampling)
Chain 3 Iteration: 950 / 1500 [ 63%] (Sampling)
Chain 2 Iteration: 751 / 1500 [ 50%] (Sampling)
Chain 4 Iteration: 950 / 1500 [ 63%] (Sampling)
Chain 1 Iteration: 950 / 1500 [ 63%] (Sampling)
Chain 3 Iteration: 1050 / 1500 [ 70%] (Sampling)
Chain 4 Iteration: 1050 / 1500 [ 70%] (Sampling)
Chain 1 Iteration: 1050 / 1500 [ 70%] (Sampling)
Chain 3 Iteration: 1150 / 1500 [ 76%] (Sampling)
Chain 2 Iteration: 850 / 1500 [ 56%] (Sampling)
Chain 4 Iteration: 1150 / 1500 [ 76%] (Sampling)
Chain 1 Iteration: 1150 / 1500 [ 76%] (Sampling)
Chain 3 Iteration: 1250 / 1500 [ 83%] (Sampling)
Chain 4 Iteration: 1250 / 1500 [ 83%] (Sampling)
Chain 1 Iteration: 1250 / 1500 [ 83%] (Sampling)
Chain 2 Iteration: 950 / 1500 [ 63%] (Sampling)
Chain 3 Iteration: 1350 / 1500 [ 90%] (Sampling)
Chain 4 Iteration: 1350 / 1500 [ 90%] (Sampling)
Chain 1 Iteration: 1350 / 1500 [ 90%] (Sampling)
Chain 3 Iteration: 1450 / 1500 [ 96%] (Sampling)
Chain 3 Iteration: 1500 / 1500 [100%] (Sampling)
Chain 3 finished in 755.1 seconds.
Chain 4 Iteration: 1450 / 1500 [ 96%] (Sampling)
Chain 1 Iteration: 1450 / 1500 [ 96%] (Sampling)
Chain 2 Iteration: 1050 / 1500 [ 70%] (Sampling)
Chain 4 Iteration: 1500 / 1500 [100%] (Sampling)
Chain 4 finished in 778.1 seconds.
Chain 1 Iteration: 1500 / 1500 [100%] (Sampling)
Chain 1 finished in 779.8 seconds.
Chain 2 Iteration: 1150 / 1500 [ 76%] (Sampling)
Chain 2 Iteration: 1250 / 1500 [ 83%] (Sampling)
Chain 2 Iteration: 1350 / 1500 [ 90%] (Sampling)
Chain 2 Iteration: 1450 / 1500 [ 96%] (Sampling)
Chain 2 Iteration: 1500 / 1500 [100%] (Sampling)
Chain 2 finished in 1003.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 829.0 seconds.
Total execution time: 1003.4 seconds.Let’s check the \(\hat{R}\) values:
Rhat4
Min. :0.9989
1st Qu.:0.9997
Median :1.0001
Mean :1.0003
3rd Qu.:1.0008
Max. :1.0056 They look OK.
Compare the varying intercepts model and a model that ignores individuals, using both WAIC/LOO and posterior predictions.
mean sd 5.5% 94.5% n_eff Rhat4
bIC -1.6683595 0.10067796 -1.8280428 -1.5044902 2041.316 1.001806
bIA -0.5603385 0.08092598 -0.6881210 -0.4302237 1751.210 1.000439
bI -0.3835373 0.05848220 -0.4764278 -0.2909250 1519.676 1.000894
bC -0.4521763 0.07003289 -0.5622873 -0.3377944 1938.544 1.002460
bA -0.6484359 0.05691941 -0.7385056 -0.5594558 1960.843 1.000483
sigma 1.9175789 0.08277129 1.7891569 2.0527683 2816.559 1.000350We estimate the sigma to be very large, indicating lots of variations in the responses among the individuals. Once we control for this average response per individual, we can estimate all the other parameters much more easily.
WAIC SE dWAIC dSE pWAIC weight
model_varying 31057.66 179.39096 0.000 NA 356.31980 1
model_no_varying 36930.02 79.88204 5872.354 173.3291 10.94063 0It seems that the expected performance out of sample, for the model with varying intercepts, is a lot better than the expected for the model with no varying intercept.