Probability calibration refers to a manner of evaluating forecasts: the forecast frequency of an event should correspond to the correct frequency of the event happening in real life. Is this truly the mark of a good analysis? Under fat-tails, Nassim Taleb in his book answer with a categorical response NO!
Probability calibration in the real world
Probability calibration amounts, in the real world, to a binary payoff: a fixed sum is paid off if the event happens. If one wants to hedge the risk of a fat-tailed variable, the question is then: which lump sum?
The answer: there is no possible lump sum that can hedge the exposure to a fat-tailed variable. The reason is the same as to why single-point forecasts are useless:
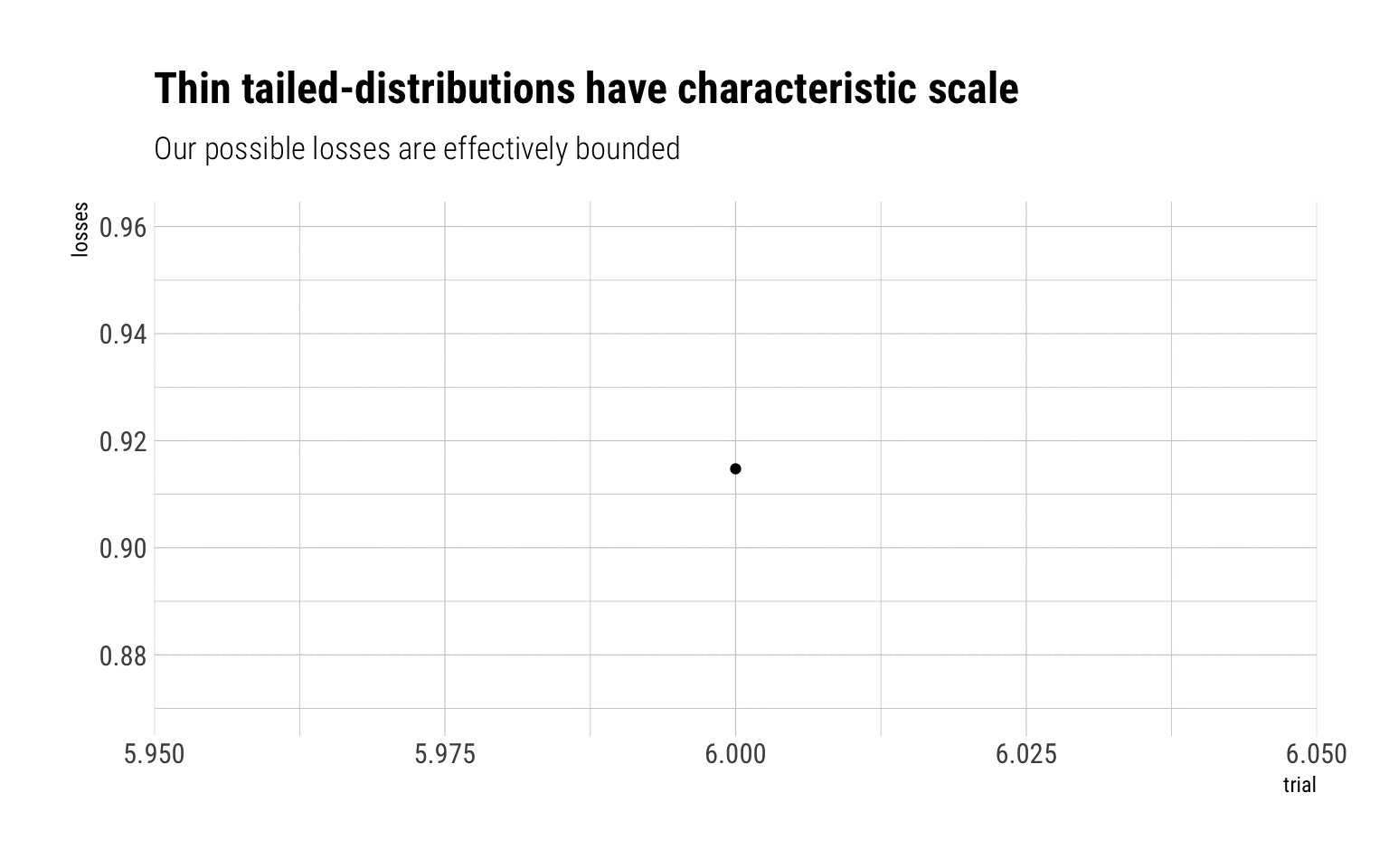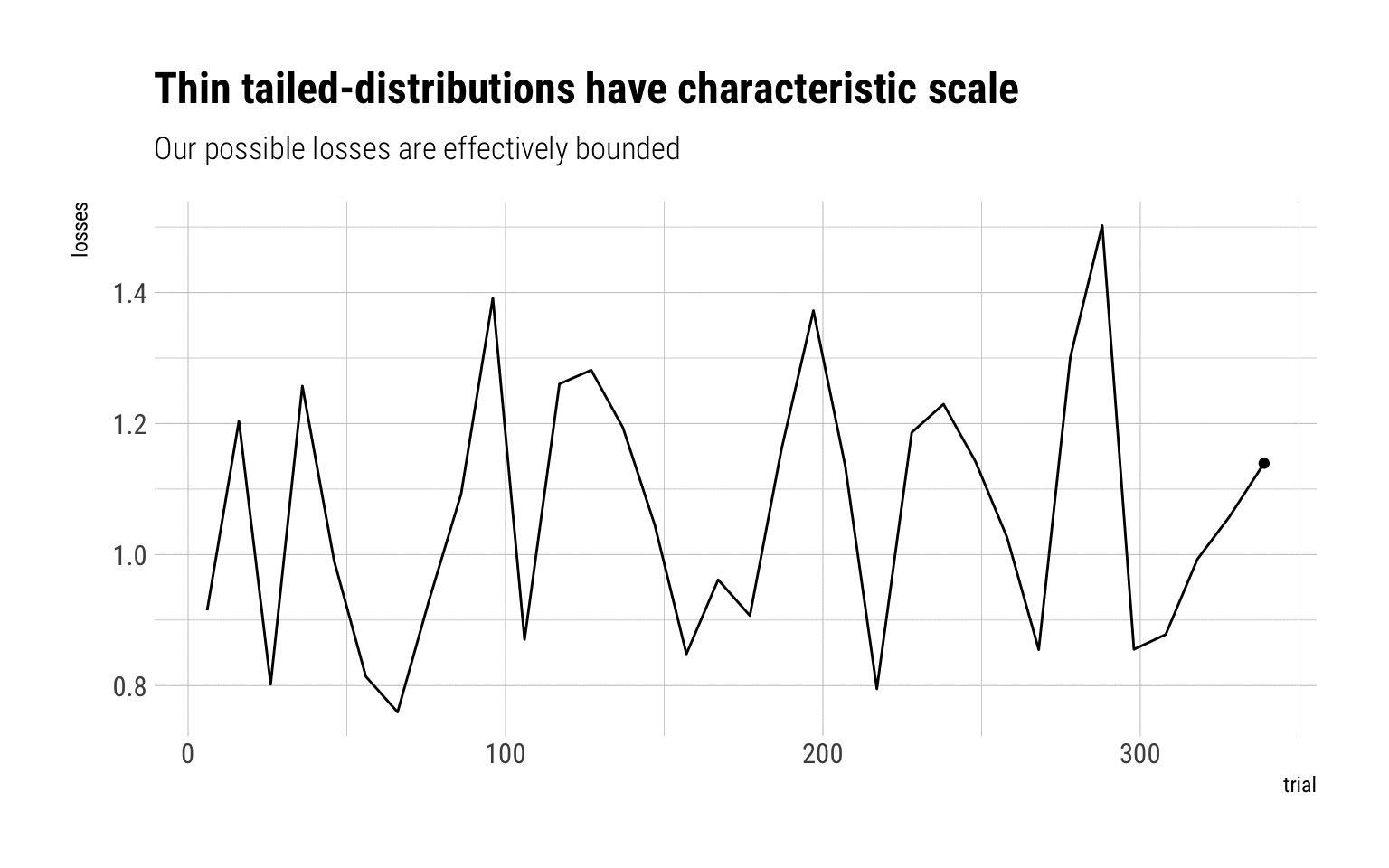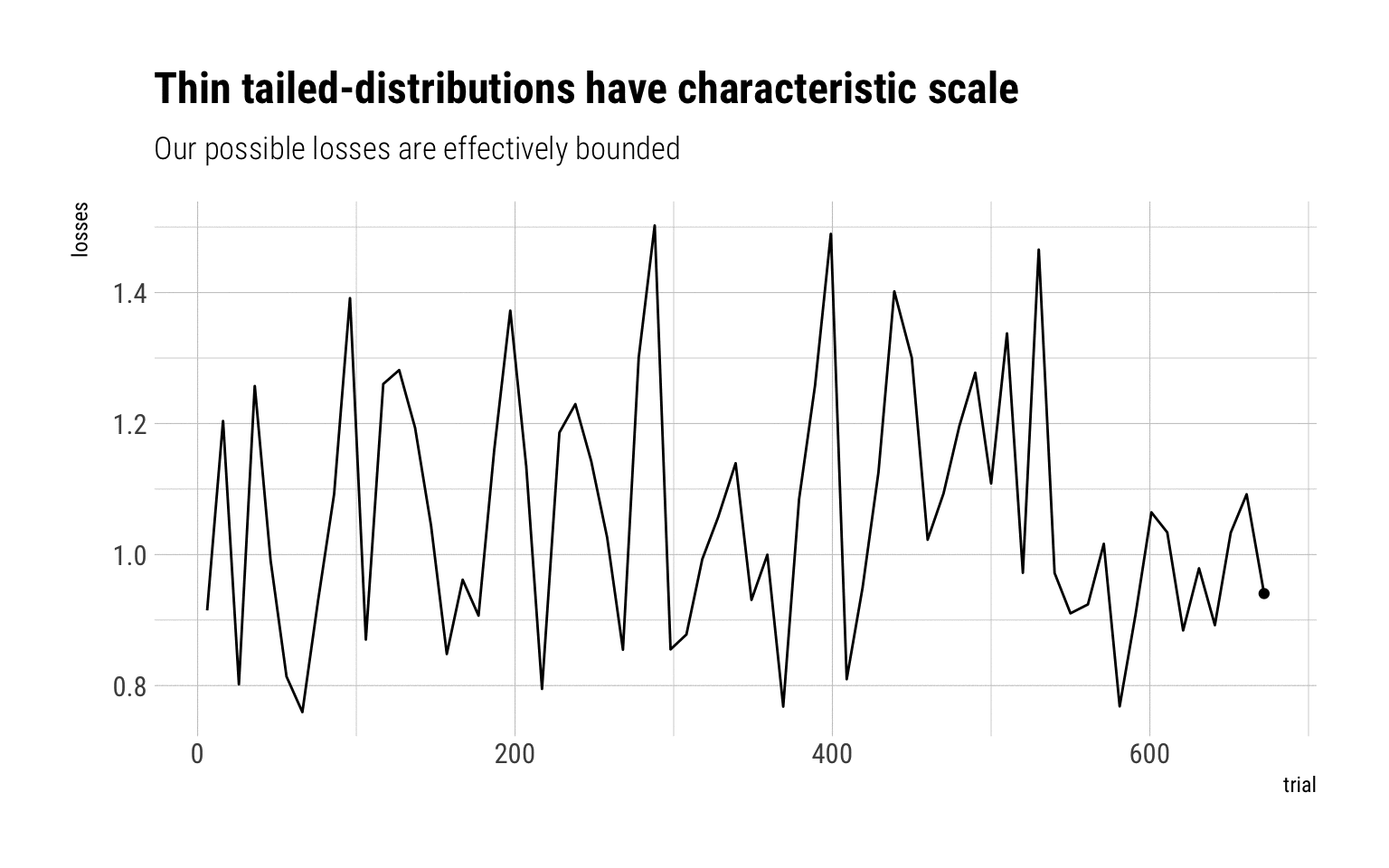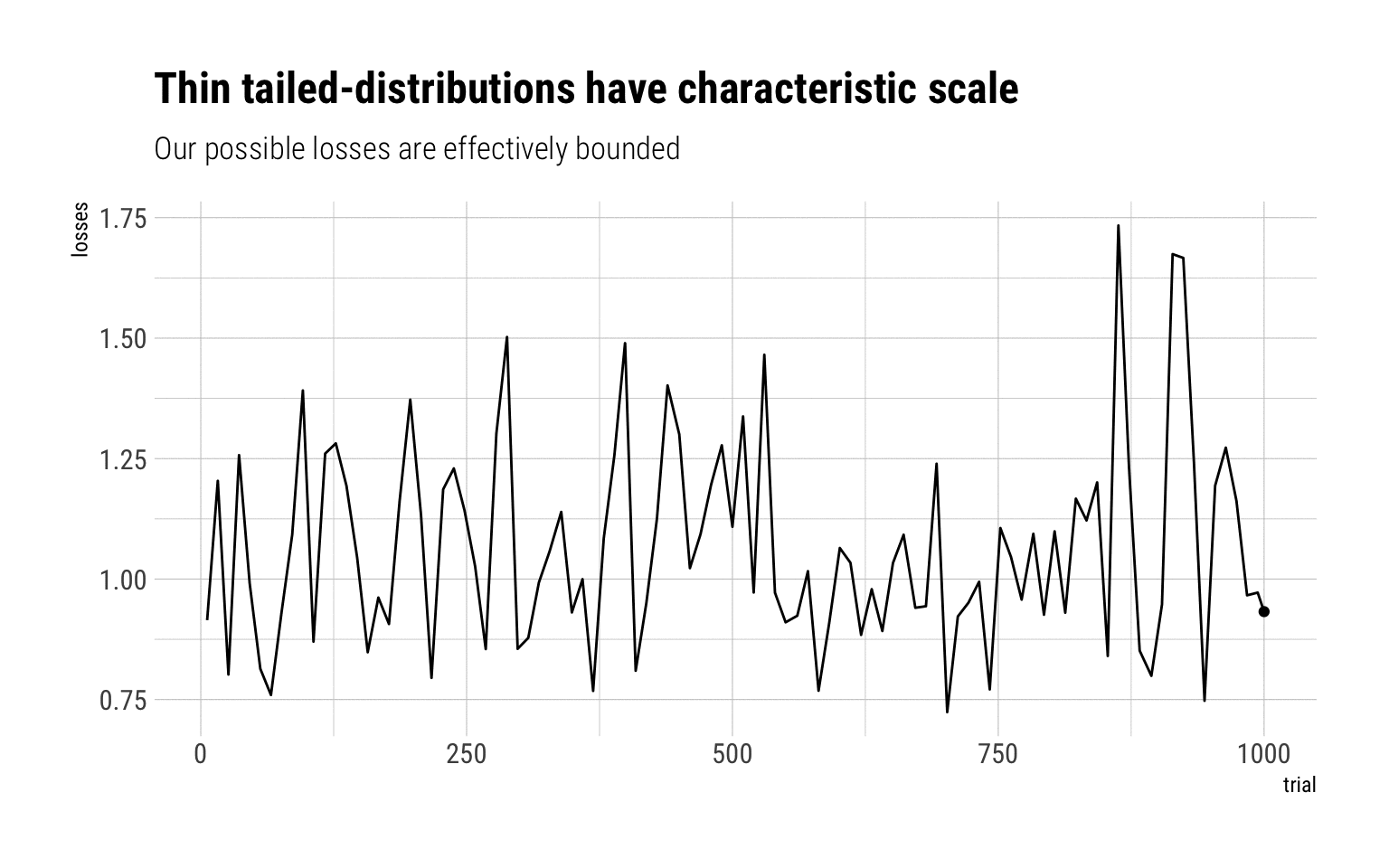
There is no typical collapse or disaster, owing to the absence of characteristic scale
Therefore, given that there is no characteristic scale for fat-tailed variables, one cannot know in advance the size of the collapse nor how much the lump sum of the binary payoff should be.
Monte Carlo simulation
A quick Monte-Carlo Simulation should do the trick to understand why fat-tailed variables have no characteristic scale. Imagine you are exposed to certain losses. You take a lump-sum insurance. Let’s simulate the possible losses that you may incur if the exposure is a lognormal. For low-values of \(\sigma\), the lognormal behaves as a Gaussian. For higher values, it behaves like a fat-tailed variable.
Log normal, sigma = 0.2
With a log normal of sigma = 0.2, a lump-sum of 2 will absolutely cover any of the losses. The reason: the MDA is Gumbel that decays pretty rapidly. Therefore, the sample maxima is effectively bounded at large values from the mean.
Whereas if we are exposed to a Pareto 80/20, there’s no lump sum that can covers us. The MDA is a Fréchet that decays as a power law:

Given this lack of characteristic scale, there should not be any prize for saying that a there will be a loss larger than \(K\). With fat-tailed variables, almost any larger value is likely. Indeed, fat-tailed variables are long-tailed variables and thus share the following property:
\[ \lim_{x \to \infty} \Pr[X>x+t\mid X>x] =1 \]
That is, reducing the variability of a fat-tailed random variable to a binary payoff makes no sense. Therefore, probability calibration with fat-tailed variables makes no sense.
Conclusion
You do not eat forecasts, most business have severly skewed payoffs, so being calibrated in probability is meaningless.